摘自：Geatpy官方教程

Geatpy 是国内华南农业大学、暨南大学、华南理工大学三所高校联合编写的基于 Python 编程语言的遗传算法工具箱。初学者可以使用该工具箱简单高效地实现遗传算法。

Geatpy 拥有两种编程模式来实现遗传算法，分别是脚本编程和面向对象编程。 # 脚本编程法

脚本编程法类似于 MATLAB 的编程风格，易于理解，但是代码量较大。

可以通过一个实例来演示脚本编程的主要流程：

假设求解 McCormick 函数的最小值。这个函数是一个二元函数，表达式为： \[ f(x,y)=\sin(x+y)+(x-y)^2-1.5x+2.5y+1 \] 这个函数具有一个全局极小点：\(f(-0.54719,-1.54719)=-1.9133\)，函数图像如下：

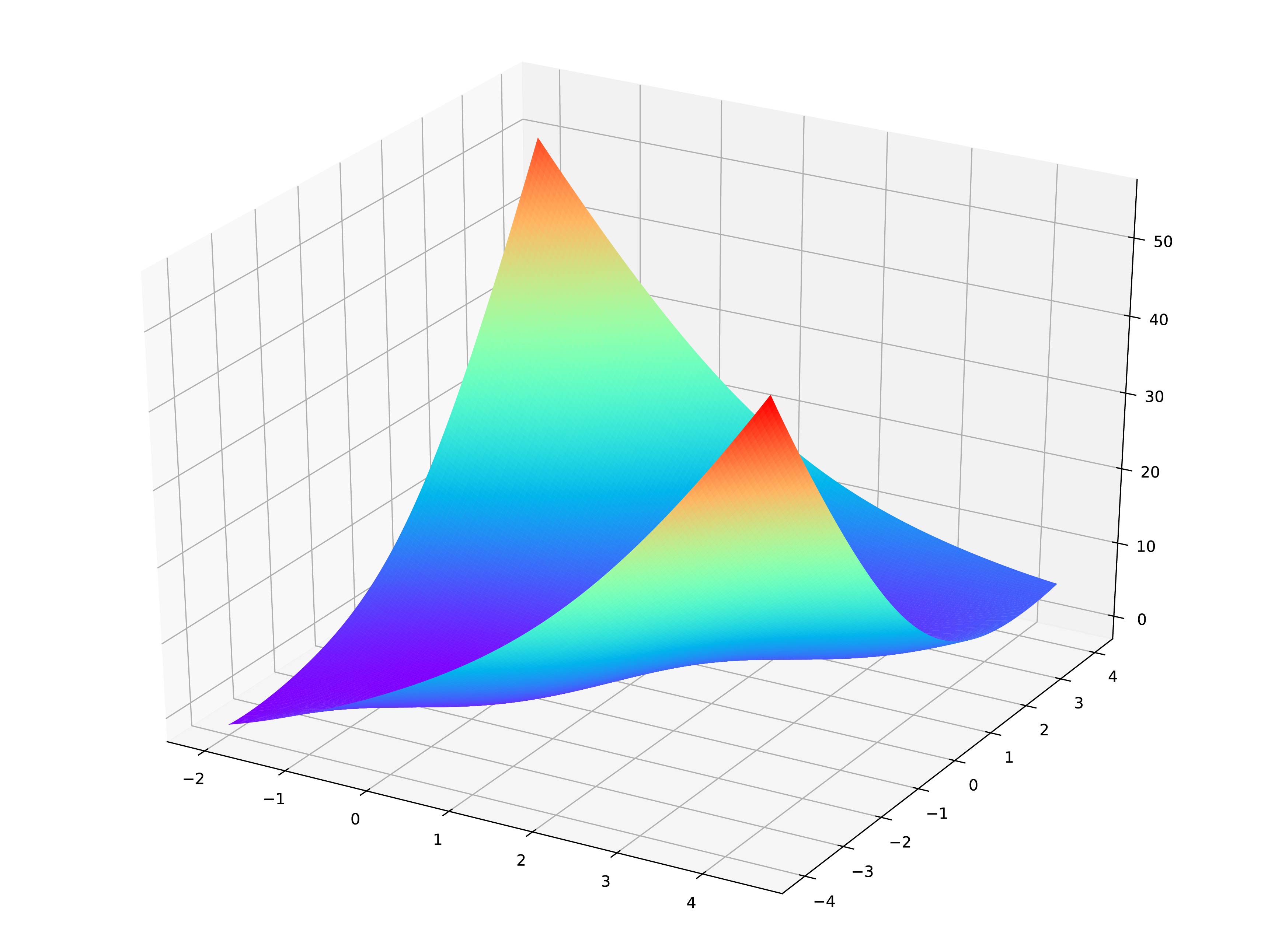
此处算法选择带有精英保留的遗传算法“Elitist Reservation GA"，可编写以下执行脚本：

# -*- coding: utf-8 -*-
"""demo.py"""
import numpy as np
import geatpy as ea  # 导入geatpy库
import time


# ===================== 目标函数设置 =======================
def aim(Phen):  # 传入种群染色体矩阵解码后的基因表现型矩阵
    x1 = Phen[:, [0]]
    x2 = Phen[:, [1]]
    return np.sin(x1 + x2) + (x1 - x2)**2 - 1.5 * x1 + 2.5 * x2 + 1


# ===================== 变量设置 ===========================
# 变量的范围
x1 = [-1.5, 4]
x2 = [-3, 4]
# 变量范围边界，1表示闭区间，0表示开区间
b1 = [1, 1]
b2 = [1, 1]
# 生成变量范围矩阵，第一行为上界，第二行为下界
ranges = np.vstack([x1, x2]).T
# 生成变量边界矩阵
borders = np.vstack([b1, b2]).T
# 变量类型，0表示连续变量，1表示离散变量
varTypes = np.array([0, 0])

# =================== 染色体编码设置 =========================
Encoding = 'BG'  # 'BG'表示采用二进制/格雷码
codes = [1, 1]  # 编码方式，1表示格雷码编码
precisions = [6, 6]  # 精度，解码后精确到小数点后的位数
scales = [0, 0]  # 0表示算术刻度，1表示对数刻度
# 调用函数创建译码矩阵
FieldD = ea.crtfld(Encoding, varTypes, ranges, borders, precisions, codes, scales)

# ==================== 遗传算法参数设置 =======================
NIND = 20  # 种群个体数目
MAXGEN = 100  # 最大遗传代数
maxormins = [1]  # 1表示最小化目标函数，-1表示最大化目标函数
selectStyle = 'sus'  # 采用随机抽样选择
recStyle = 'xovdp'  # 采用两点交叉
mutStyle = 'mutbin'  # 采用二进制染色体变异算子
pc = 0.9  # 交叉概率
pm = 1  # 整条染色体变异概率（每一位变异的概率 = pm / 染色体长度）
Lind = int(np.sum(FieldD[0, :]))  # 计算染色体长度
obj_trace = np.zeros((MAXGEN, 2))  # 定义目标函数值记录器
var_trace = np.zeros((MAXGEN, Lind))  # 定义染色体记录器

# ==================== 开始进行遗传进化 =======================
start_time = time.time()  # 开始计时
Chrom = ea.crtpc(Encoding.NIND, FieldD)  # 生成种群染色体矩阵
variable = ea.bs2real(Chrom, FieldD)  # 对初始种群进行解码
ObjV = aim(variable)  # 计算初始种群个体的目标函数值
best_ind = np.argmin(ObjV)  # 计算当代最有个体的序号

# 开始进化
for gen in range(MAXGEN):
    FitnV = ea.ranking(maxormins * ObjV)  # 根据目标函数大小分配适应度值
    SelCh = Chrom[ea.selecting(selectStyle, FitnV, NIND - 1)]  # 选择
    SelCh = ea.recombin(recStyle, SelCh, pc)  # 重组
    SelCh = ea.mutate(mutStyle, Encoding, SelCh, pm)  # 变异
    # 把父代精英个体与自带的染色体进行合并，得到新一代种群
    Chrom = np.vstack([Chrom[best_ind, :], SelCh])
    Phen = ea.bs2real(Chrom, FieldD)  # 对种群进行解码
    ObjV = aim(Phen)  # 求种群个体的目标函数值
    best_ind = np.argmin(ObjV)  # 当代最优个体的序号
    obj_trace[gen, 0] = np.sum(ObjV) / ObjV.shape[0]  # 记录当代种群的目标函数均值
    obj_trace[gen, 1] = ObjV[best_ind]  # 记录当代种群最优个体的目标函数值
    var_trace[gen, :] = Chrom[best_ind, :]  # 记录当代种群最优个体的染色体

# 进化完成
end_time = time.time()  # 结束计时
ea.trcplot(obj_trace, [['种群个体平均目标函数值', '种群最优个体目标函数值']])  # 绘制图像

# ===================== 输出结果 ==============================
best_gen = np.argmin(obj_trace[:, [1]])
print('最优解的目标函数值：', obj_trace[best_gen, 1])
variable = ea.bs2real(var_trace[[best_gen], :], FieldD)  # 解码得到表现型（变量值）
print('最优解的决策变量值为：')
for i in range(variable.shape[1]):
    print('x'+str(i)+'=', variable[0, i])
print('用时：', end_time - start_time, '秒')

面向对象编程法

面向对象编程法通过实例化进化算法框架来完成实际编程。

Geatpy 进化算法框架包含四个大类，分别是：

算法模板类 (Algorithm)
种群类 (Population)
多染色体混合编码种群类 (PsyPopulation)
问题类 (Problem)

其中，Population 类和 PsyPopulation 类需要进行实例化，Algorithm 类和 Problem 类需要进行继承。

以下通过两个示例演示面向对象编程法的编程过程：

例1：带约束的单目标优化问题

问题模型：

\[ \begin{cases} \max f(x_1, x_2, x_3)=4x_1+2x_2+x_3\\ \text{s.t.}\quad 2x_1+x_2\leq 1\\ \quad \quad \ \ x_1+2x_3\leq 2\\ x_1\in[0,1],\quad x_2\in[0,1],\quad x_3\in(0,2) \end{cases} \]
全局最优解：\(f(0.5,0,0.5)=2.5\)
方法：差分进化算法“DE/best/1/L"

代码实现如下：

通过继承 Problem 类描述问题模型： “MyProblem1.py" 文件：

# -*- coding: utf-8 -*-
"""MyProblem1.py"""
import numpy as np
import geatpy as ea


class MyProblem1(ea.Problem):  # 继承Problem类
    def __init__(self):
        name = 'MyProblem'  # 函数名称
        M = 1  # 目标维数
        maxormins = [-1]  # 最小最大化标记列表，1为最小化，-1为最大化
        Dim = 3  # 变量维数
        varTypes = [0] * Dim  # 变量类型，0为连续，1为离散
        lb = [0, 0, 0]  # 变量下界
        ub = [1, 1, 2]  # 变量上界
        lbin = [1, 1, 0]  # 变量上边界
        ubin = [1, 1, 0]  # 变量下边界
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes,
                            lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数，传入种群对象
        Vars = pop.Phen  # 决策变量矩阵
        # 变量列向量
        x1 = Vars[:, [0]]
        x2 = Vars[:, [1]]
        x3 = Vars[:, [2]]
        pop.ObjV = 4 * x1 + 2 * x2 + x3  # 目标函数值
        # 生成违反约束程度矩阵，小于或等于零满足约束，大于零违反约束
        pop.CV = np.hstack([2 * x1 + x2 - 1,  # 第一个约束
                           x1 + 2 * x3 - 2,  # 第二个约束
                           np.abs(x1 + x2 + x3 - 1)])  # 第三个约束

上述程序使用了可行性法定义约束条件，也可使用罚函数法定义：

def aimFunc(self, pop):
    Vars = pop.Phen  # 决策变量矩阵
    # 变量列向量
    x1 = Vars[:, [0]]
    x2 = Vars[:, [1]]
    x3 = Vars[:, [2]]
    pop.ObjV = 4 * x1 + 2 * x2 + x3  # 目标函数值
    # 采用罚函数法处理约束
    exIdx1 = np.where(2 * x1 + x2 > 1)[0]  # 找到违反约束一的个体
    exIdx2 = np.where(x1 + 2 * x3 > 2)[0]  # 找到违反约束二的个体
    exIdx3 = np.where(x1 + x2 + x3 != 1)[0]  # 找到违反约束三的个体
    exIdx = np.unique(np.hstack([exIdx1, exIdx2, exIdx3]))  # 合并索引
    alpha = 2  # 惩罚缩放因子
    beta = 1  # 惩罚最小偏移量
    f[exIdx] += self.maxormins[0] * alpha * (np.max(f) - np.min(f) + beta)
    pop.ObjV = f  # 将目标函数值矩阵赋给种群的ObjV属性

编写执行脚本调用模板进行求解 “main1.py”文件：

# -*- coding: utf-8 -*-
"""main1.py"""
import numpy as np
import geatpy as ea
from MyProblem1 import MyProblem1

# ============================== 实例化问题对象 =================================
problem = MyProblem1()

# ================================= 种群设置 ===================================
Encoding = 'RI'  # 编码方式
NIND = 50  # 种群规模
# 创建区域描述器
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)
# 实例化种群对象
population = ea.Population(Encoding, Field, NIND)

# =============================== 算法参数设置 ==================================
# 实例化模板对象
myAlgorithm = ea.soea_DE_best_1_L_templet(problem, population)
myAlgorithm.MAXGEN = 1000  # 最大遗传代数
myAlgorithm.mutOper.F = 0.5  # 设置差分进化的变异缩放因子
myAlgorithm.recOper.XOVR = 0.5  # 设置交叉概率
myAlgorithm.drawing = 1  # 设置绘图方式，0为不绘图，1为绘制结果图，2为绘制进化过程动态图

# ========================== 调用算法模板进行种群进化 =============================
[population, obj_trace, var_trace] = myAlgorithm.run()  # 执行算法模板
# 输出结果
best_gen = np.argmax(obj_trace[:, 1])
best_ObjV = obj_trace[best_gen, 1]
print('最优的目标函数值为：%s' % (best_ObjV))
print('最优的决策变量值为：')
for i in range(var_trace.shape[1]):
    print(var_trace[best_gen, i])
print('有效进化代数：%s' % (obj_trace.shape[0]))
print('最优的一代是第%s代' % (best_gen + 1))
print('评价次数：%s' % (myAlgorithm.evalsNum))
print('时间已过%s秒' % (myAlgorithm.passTime))

例2：带约束的多目标优化问题

问题： \[ \min= \begin{cases} f_1(x,y)=4x^2+4y^2\\ f_2(x,y)=4(x-5)^2+4(y-5)^2 \end{cases}\\ \text{s.t.}= \begin{cases} g_1(x,y)=(x-5)^2+y^2\leq25\\ g_2(x,y)=(x-8)^2+(y-3)^2\geq7.7\\ 0\leq x\leq 5,\quad 0\leq y\leq 3 \end{cases} \]

问题类：

# -*- coding: utf-8 -*-
"""MyProblem2.py"""
import numpy as np
import geatpy as ea


class MyProblem2(ea.Problem):
    def __init__(self):
        name = 'BNH'  # 函数名称
        M = 2  # 目标维数
        maxormins = [1] * M  # 最大、最小
        Dim = 2  # 变量维数
        varTypes = [0] * Dim  # 变量类型
        lb = [0] * Dim  # 变量下界
        ub = [5, 3]  # 变量上界
        lbin = [1] * Dim  # 变量下边界
        ubin = [1] * Dim  # 变量上边界
        # 调用父类构造方法
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub,
                            lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到变量矩阵
        x1 = Vars[:, [0]]
        x2 = Vars[:, [1]]
        f1 = 4 * x1**2 + 4 * x2**2
        f2 = (x1 - 5)**2 + (x2 - 5)**2
        # 采用可行性法则处理约束
        pop.CV = np.hstack([(x1 - 5)**2 + x2**2 - 25,
                            -(x1 - 8)**2 - (x2 - 3)**2 + 7.7])
        # 把求得的目标函数赋给种群pop的ObjV
        pop.ObjV = np.hstack([f1, f2])

    def calBest(self):  # 计算全局最优解
        N = 10000  # 遇得到10000个真实帕累托前沿点
        x1 = np.linspace(0, 5, N)
        x2 = x1.copy()
        x2[x1 >= 3] = 3
        return np.vstack((4 * x1**2 + 4 * x2**2, (x1 - 5)**2 + (x2 - 5)**2)).T

执行脚本：

# -*- coding: utf-8 -*-
"""main2.py"""
import geatpy as ea
from Myproblem2 import MyProblem2

# =============================== 实例化问题对象 ================================
problem = MyProblem2()

# ================================== 种群设置 ==================================
Encoding = "RI"  # 编码方式
NIND = 100  # 种群规模
# 创建区域描述器
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)
# 实例化种群对象
population = ea.Population(Encoding, Field, NIND)

# =============================== 算法参数设置 ==================================
# 实例化算法模板对象
myAlgorithm = ea.moea_NSGA2_templet(problem, population)
myAlgorithm.MAXGEN = 200  # 最大遗传代数
myAlgorithm.drawing - 1  # 绘图方式

# =========================== 调用算法模板进行种群进化 ============================
# 调用run执行算法模板，得到帕累托最优解集NDSet。
# NDSet是一个种群类Population的对象。
# NDSet.ObjV为最优解个体的目标函数值；NDSet.Phen为对应的决策变量值。
# 详见Population.py中关于种群类的定义。
NDSet = myAlgorithm.run()  # 执行算法模板，得到非支配种群
NDSet.save()  # 把结果保存到文件中
# 输出
print('用时：%f秒' % (myAlgorithm.passTime))
print('评价次数：%d次' % (myAlgorithm.evalsNum))
print('非支配个体数：%d个' % (NDSet.sizes))
print('单位时间找到帕累托前沿点个数：%d个' % (int(NDSet.sizes // myAlgorithm.passTime)))
# 计算指标
PF = problem.getBest()  # 获取真实前沿
if PF is not None and NDSet.sizes != 0:
    GD = ea.indicator.GD(NDSet.ObjV, PF)  # 计算GD指标
    IGD = ea.indicator.IGD(NDSet.ObjV, PF)  # 计算IGD指标
    HV = ea.indicator.HV(NDSet.ObjV, PF)  # 计算HV指标
    Spacing = ea.indicator.Spacing(NDSet.ObjV)  # 计算Spacing指标
    print('GD: %f' % GD)
    print('IGD: %f' % IGD)
    print('HV: %f' % HV)
    print('Spacing: %f' % Spacing)

# ======================== 进化过程指标追踪分析 ==================================
if PF is not None:
    metricName = [['IGD'], ['HV']]
    [NDSet_trace,
     Metrics] = ea.indicator.moea_tracking(myAlgorithm.pop_trace, PF,
                                           metricName, problem.maxormins)
    # 绘制指标追踪分析图
    ea.trcplot(Metrics, labels=metricName, titles=metricName)

donghao_34's Blog

遗传算法学习笔记（二）——使用 Geatpy 工具箱

面向对象编程法

例1：带约束的单目标优化问题

例2：带约束的多目标优化问题