摘自:
- https://www.jianshu.com/p/ae5157c26af9
- https://blog.csdn.net/u010451580/article/details/51178225
- http://geatpy.com/index.php/ea_introduction/
遗传算法是一种模拟达尔文物种进化理论的算法,算法很新颖独特。
原理
遗传算法模拟了自然界物竞天择的生物进化过程。
它的主要过程是由代表问题的潜在解集的一个种群 (population) 开始。种群由经过基因 (gene) 编码 (coding) 的一定数目的个体 (individual) 组成。每个个体实际上是染色体 (chromosome) 带有特征的实体。
随后以面为单位搜索,通过随机初始化种群,并按照适者生存、优胜劣汰的原理,主带逐代 (generation) 演化产生越来越好的近似解。在每一代中,根据个体的适应度 (fitness) 大小来选择 (selection) 个体,并借助于自然遗传学中的遗传算子 (genetic operators) 进行组合交叉 (crossover) 和变异 (mutation),产生出新的解集的种群。
实现过程
遗传算法的实现过程可以由下图表示:
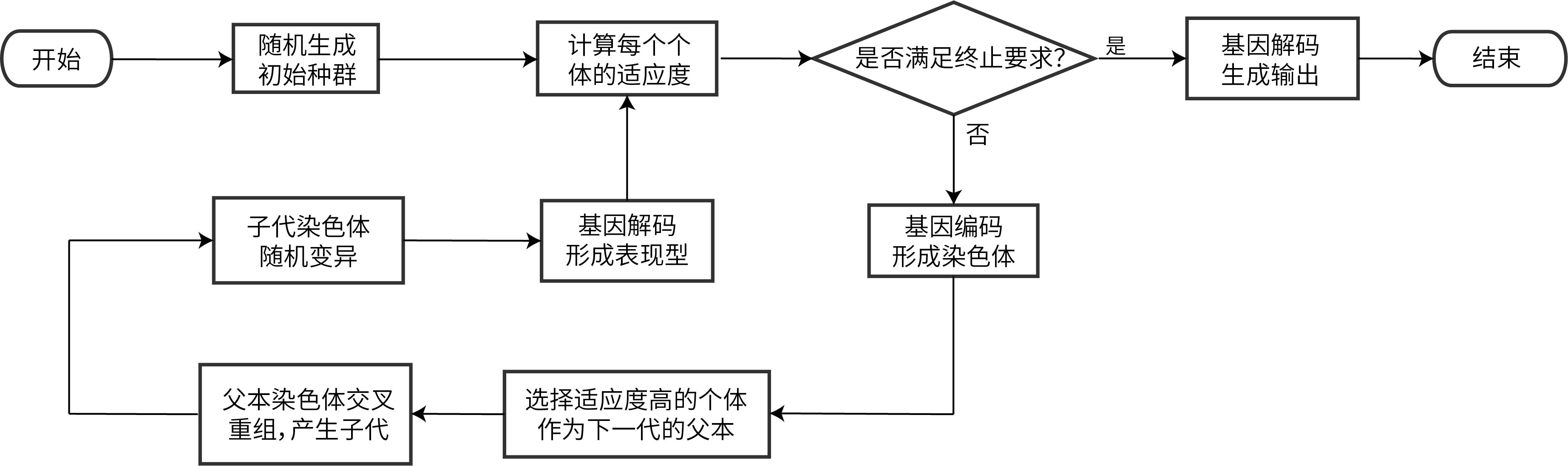
编码
二进制编码: 使用类似于模数转换的公式: \[ x = -1 + x^t\frac{b-a}{2^n-1} \] 其中,\(x^t\)为二进制数的十进制整数值,\(a\)和\(b\)表示对应浮点数区间的左右端点,\(n\)为二进制数的位数。
浮点数编码:
符号编码
适应性评分与选择函数
- 物竞——适应性函数:用以评判个体适应程度的函数:
- 目标函数适应度: 直接使用目标函数值作为适应度数值,实现简单直接;
- 目标函数变换适应度: 使用某种变换对目标函数值进行加工,作为适应度数值;
- 基于等级划分的适应度分配计算 (Rank-based fitness assignment): 将个体按照目标函数大小进行排序,之后按照顺序对个体赋予适应度评分。可以避免目标函数数值带来的放缩不当的问题。排序方法包括线性排序和非线性排序等。
- 天择——选择函数:根据适应值确定个体繁殖后代的概率:
- 轮盘赌选择 (Roulette Wheel Selection, RWS): 每个个体进入下一代的概率等于其适应度值与种群总适应度值的比例,误差较大。
- 随机竞争选择 (Stochastic Tournament): 每次按轮盘赌方法选择一对个体,让两个个体进行竞争,适应度高的选中,如此反复,直到选满为止。
- 最佳保留选择: 按照轮盘赌方法选择,之后再将适应度最高的个体完整复制到下一代群体中。
- 无回放随机选择(或期望值选择,Excepted Value Selection):
- 计算每个个体在下一代的生存期望数目;
- 若某个体参与交叉运算,则期望数目减去0.5,若未参与交叉运算,则期望数目减去1.0;
- 随着选择过程的进行,当个体的生存期望数目小于0时,该个体不再有机会被选中。
- 确定式选择:
- 计算每个个体在下一代的生存期望数目;
- 用的整数部分确定个体再下一代的生存数目;
- 用的小数部分对个体进行降序排列,顺序选取前个个体加入到下一代中。
- 无回放余数随机选择: 确保适应度大于平均值的个体能够遗传,误差较小。
- 均匀排序: 按照适应度大小排序,按照排序分配选中概率。
- 最佳保存策略: 适应度最高的个体不参与交叉和变异运算,用以代替经交叉、变异操作后适应度最低的个体。
- 随机联赛选择: 每次选取几个个体中适应度最高的一个个体遗传到下一代。
- 排挤选择: 新生的子代代替或排挤相似的旧父代个体,提高群体多样性。
遗传变异
基因重组/交叉
单点交叉:选取一点;
两点交叉:选取两点;
多点交叉:选取多点;
均匀交叉:概率等同;
算术交叉:线性组合(常用于浮点数编码)。
(注:二进制交叉:交换位;浮点数交叉:取二者之间的随机值)
基因突变
基本位变异:选取一位或多位;
均匀变异:设置一个一定范围内的随机数,以一个较小的概率替换基因上的原有基因值;
边界变异:随机选取两个边界基因值之一替代原有基因值;
非均匀变异:对原基因值做随机扰动,对每位都以相同的概率进行变异运算,将扰动结果作为新基因值;
高斯近似变异:使用关于原基因高斯分布的一个随机数替代元基因值。
(注:二进制变异:反转0、1;浮点数变异:增加或减少一个小的随机数(步长))