基于小波分解主元分析法建立的激光焊接信号分析模型
You D, Gao X, Katayama S. WPD-PCA-based laser welding process monitoring and defects diagnosis by using FNN and SVM[J]. IEEE Transactions on Industrial Electronics, 2014, 62(1): 628-636.
光敏二极管和分光计是两种结构简单、成本低廉的光信号捕捉设备。
光信号分析的常用方法:
- 主元素分析法 (principal component analysis, PCA)
- 偏最小二乘法 (partial least square, PLS)
- 支持向量机 (support vector machine, SVM)
小波包分解主元素分析法 (Wavelet packet decomposition PCA, WPD-PCA)
使用 WPD-PCA 方法提取焊接信号中的特征参数,焊接信号包括光电二极管采集到的高频信号和分光计采集到的低频信号。 并使用图像处理的方法来量化焊接状态,确定焊接几何参数。使用前向神经网络来建立光信号和几何参量的关系模型, 使用支持向量机建立光信号和焊接缺陷的关系模型。
光电二极管被用来测量可见光 (350--750 nm)和激光反射 (1030 nm)。分光计可以用来测量光谱数据 (186--1100 nm)。
光电二极管信号的特征提取
离散小波分解被用于多尺度信号分析,但只能得到分解的低频(近似)系数 (approximation coefficients)。 WPD (小波包分解)是这种方法的延伸,它使用低通、高通滤波器对低频系数和高频(细节)系数 (detail coefficients).
小波包分解的表达式如下所示: \[ W_{j, k}^n(t)=2^{j/2}W^n(2^jt-k),\qquad j, k\in Z. \] 式中 \(j\) 和 \(k\) 表示尺度等级。\(j\) 表示缩放等级,控制小波的频域特性;\(k\) 表示平移等级,控制小波的频域特性。
使用 Daubechies 母小波 (db10),尺度函数和母小波可以由下式表示: \[ W_{0,0}^0(t)=\phi(t)\quad W_{0,0}^1(t)=\psi(t). \] 低通和高通滤波器可以由下式定义: \[ h(k)=\langle\phi(t),\phi(2t-k)\rangle\quad g(k)=\langle\psi(t),\phi(2t-k)\rangle. \]
因此,\(n>1\) 情况下的小波包方程可以由下式描述: \[ W_{j,k}^{2n}(t)=\sqrt{2}\sum_kh(k)W_{j-1,k}^n(2t-k), \]
\[ W_{j,k}^{2n+1}(t)=\sqrt{2}\sum_kg(k)W_{j-1,k}^n(2t-k). \]
光电二极管信号 \(\boldsymbol{x}_p\) 的小波包系数为 \[ Cp_j^n(k)=\sum_t\boldsymbol{x}_p(t)W_{j,k}^n(t). \] 使用小波包分解分别获得可见光信号和激光反射光信号的小波包系数 \(Cpv_j^n(k)\) 和 \(Cpr_j^n(k)\),从尺度的系数获得其特征向量 \(\boldsymbol{X}pv_{j,n}\) 和 \(\boldsymbol{X}pr_{j,n}\),最终得到光电二极管的特征向量组 \(\boldsymbol{V}_P\),其中 \[ \boldsymbol{V}_P=[\boldsymbol{X}pv_{j,1},\boldsymbol{X}pv_{j,2},\dots,\boldsymbol{X}pv_{j,N_s},\boldsymbol{X}pr_{j,1},\boldsymbol{X}pr_{j,2},\dots,\boldsymbol{X}pr_{j,N_s}]. \] 其中,\(n=1\sim10\) 特征向量的元素可以由下式求出:
\[ X_{j,n}^1=\frac{1}{K}\sum_{k=1}^KCp_j^n(k), \]
\[ X_{j,n}^2=\sqrt{\frac{1}{K}\sum_{k=1}^K(Cp_j^n(k))^2}, \]
\[ X_{j,n}^4=\frac{\max|Cp_j^n(k)|}{X_2}, \]
\[ X_{j,n}^4=\frac{1}{K}\sum_{k=1}^{K}(Cp_j^n(k))^2, \]
\[ X_{j,n}^5=\frac{1}{K}\sum_{k=1}^{K}(Cp_j^n(k))^4, \]
\[ X_{j,n}^6=\frac{E[(Cp_j^n(k)-X_1)^3]}{X_2^3}, \]
\[ X_{j,n}^7=\frac{X_2}{X_1}, \]
\[ X_{j,n}^8=\frac{1}{K}\sum_\omega\log|\Phi_j^n(\omega)|\mathrm{e}^{2\mathrm{\pi}\omega\mathrm{i}/K}, \]
\[ X_{j,n}^9=\frac{1}{K}\sum_\omega\log|\Phi_j^n(\omega)|\mathrm{e}^{4\mathrm{\pi}\omega\mathrm{i}/K}, \]
\[ X_{j,n}^{10}=X_9-X_8. \]
其中,\(\Phi_j^n(\omega)\) 表示小波包系数 \(Cp_j^n(k)\) 的傅里叶变换。
最终得到的特征向量组 \(\boldsymbol{V}_P\) 为 \(N_s\times2\times10\) 的矩阵,\(N_s\) 为子带的数量。
分光计信号的特征提取
使用 500 Hz 的采样频率,对信号进行采样。实验发现 400--900 nm 波长范围包含了大多数特征。分光器被分解为 25 各子带,每个子带包含 20 个光谱,并将其平均值当作光谱的特征值: \[ Xs_M=\frac{\sum_{m=m_1}^{m_2}x_s^m}{20} \] 分光计的特征向量组由下式表示: \[ \boldsymbol{V}_S=[Xs_1,Xs_2,\dots,Xs_{25}] \]
主元素分析法进行特征选择
通过上述过程,共有 \(N=N_s\times2\times10+25\) 组特征被提取了出来。其中 \(N_s\) 在 1 到 4 之间,总特征向量数在 45 到 105 之间。通过特征选择可以提升模型预测和分类的泛化能力。主元素分析法 (Primary Component Analysis, PCA) 是一种常用的特征选择方法,本文使用该方法对特征向量组中的特征进行筛选。
如果每个传感器采集到的采样点数为 \(H\),那么可以对特征进行正则化,得到 \[ \hat{\boldsymbol{V}}=\frac{\boldsymbol{V}-\boldsymbol{V}_{\text{mid}}}{\frac{1}{2}(\boldsymbol{V}_{\text{max}}-\boldsymbol{V}_{\text{min}})} \] 其中 \(\boldsymbol{V}_{\text{mid}}\),\(\boldsymbol{V}_{\text{max}}\) 和 \(\boldsymbol{V}_{\text{min}}\) 分别时特征数值 \(\boldsymbol{V}\) 的中值、最小值和最大值。
PCA 方法对特征进行如下变换: \[ \boldsymbol{S}=\boldsymbol{U}^{\mathrm{T}}\hat{\boldsymbol{V}} \] 其中,\(\boldsymbol{U}\) 是一个 \(N\times N\) 的正交矩阵,他的第 \(i\) 列 \(\boldsymbol{u}_i\) 是样本协方差矩阵的第 \(i\) 个特征向量,即 \[ \boldsymbol{C}=\frac{1}{H}\hat{\boldsymbol{V}}^{\mathrm{T}}\hat{\boldsymbol{V}} \] 通过求解特征方程 \[ \lambda_i\boldsymbol{u}=\boldsymbol{Cu}_i\qquad i=1,2,\dots,N \] 可以得到矩阵 \(\boldsymbol{C}\) 的特征值 \(\lambda_i\) 和特征向量 \(\boldsymbol{u}_i\)。
于是主元素 \(\boldsymbol{S}_i\) 就是 \(\hat{\boldsymbol{V}}\) 的正交变换,即 \[ \boldsymbol{S}_i=\boldsymbol{u}_i^{\text{T}}\hat{\boldsymbol{V}} \]
视觉传感器焊缝几何特征和缺陷特征提取
焊缝几何特征提取
使用实验室尺度的视觉传感器来提取焊缝几何特征,从而确定焊接状态。飞溅特征使用视觉相机获取。匙孔表面的细微特征需要使用辅助照明 (Auxiliary Illumination, AI) 来进行观测。匙孔长度和熔池的深度的测量则使用 X 射线视觉影像技术完成。
根据图像的位置特征,可以肯容易地将飞溅特征和金属蒸汽特征分离开来,并根据运动方向(前向或后向)将飞溅进行分类。其次,匙孔尺寸和坐标信息可以通过灰度处理和二值化实现。最后,匙孔长度和熔池深度可以通过对X射线进行灰度处理来提取。使用上述三种视觉传感器中获得的图像提取了六种典型几何特征,包括前向飞溅 \(y_{sf}\),后向飞溅 \(y_{bf}\),匙孔尺寸 \(y_{ks}\),匙孔位置 \(y_{kp}\),匙孔深度 \(y_{kd}\),和熔池深度 \(y_{md}\)。因此,焊接状态参量可以由下式表示: \[ Y=[y_{sf},y_{sb},y_{ks},y_{kp},y_{kd},y_{md}] \]
焊缝缺陷特征提取
根据国际标准 EN ISO 13919-1,试验选择了三种代表性的焊接缺陷用于焊缝缺陷的分类参考。因此,焊接结果 \(y_{wr}\) 可以被分为四类。类一代表完好焊缝,类二代表爆炸,类三代表焊瘤,类四代表下凹。
预测模型的建立
基于前向神经网络预测进行过程监控
在焊接过程中,超过 20 种输入特征 \(i\) 以及 6 种焊接几何参数被用于拟合模型。模型使用了一个单隐层的神经网络,并使用了 sigmoid 传递函数作为隐藏层的传递函数。输出层的传递函数为线性函数。
弧焊过程监控研究现状
UHRLANDT D. Diagnostics of metal inert gas and metal active gas welding processes [J]. Journal of Physics D: Applied Physics, 2016, 49(31): 313001.
弧焊过程中的电测量
如今,通过将电压探头、分路器或罗氏线圈(用于电流测量)与现代快速数字记录仪相连,可以很好地测量电信号的快速变化。需要特别注意的是设备的频率响应特性、接地和屏蔽以及电压探头的测量位置。电测量的一个优点是电弧特性的所有动态变化,包括电弧附着和金属转移的影响,都会在电流-电压特性中留下线索。他的缺点则是由这些有用的信息通常会和自身以及电源和噪声重叠在一起。
即便如此,电压和电流测量与复杂的信号处理方法相结合,仍然是控制过程稳定性和焊接质量的最受欢迎的方法。这是因为这样可以避免额外的工作,例如使用光学传感器等。短路频率可以作为一个过程稳定的简单指标。而从电压信号中分辨出熔滴的分离则较为困难。
复变分析法 (Complex Analysis) 是一种分析电压和电流信号与焊接质量之间的的关系的常用方法。其分析过程常常是基于对信号时频特性和的功率谱密度的分析之上。主要的分析方法可以包括:
- 短时傅里叶变换 (Short-time Fourier Transform)
- 电压电流信号自相关函数的傅里叶变换
- 模糊逻辑分析
- 神经网络
电弧电压测量是研究电弧柱内电场和电极鞘层电压的一种方法。例如,在短路过程的实验中,通过比较已建立的电弧和短路前电弧的测量电压,以及电弧图像确定的电弧长度,可以确定电弧柱和电极鞘层区域的单独电压降。此时建议使用具有几乎恒定电压输出和低噪声的受控电源。
此外,可以直接将电子探针置于等离子体中测量电弧局部的电势或热导率,这也是直接测量此类物理量的唯一方法。电子探针可以用于研究局部等离子体的各类特征。然而,探针对等离子体的局部扰动和热等离子体探针理论的局限性,特别是无碰撞鞘层方法的有效性,使得这种方法相当困难,限制了结果的准确性。霍尔传感器也可以用于测量电弧内部的电流分布。
研究现状分析
当前工作的中心主要在两个方面:
电弧的物理性质和材料转移的改进诊断方法
包括利用电弧发射光谱对脉冲电弧等离子体内部温度等性质的二维甚至三维分布的获取等。
新的监控和控制方法
主要集中在光谱、高速摄影的应用上。类似于声音信号的其他方法收到的关注较少。
需要解决的问题
- 电弧非平衡区域(外部区域和靠近墙壁的区域)以及不符合 LTE 假设的时间段(点火、小电流电弧)中的等离子体特性——这一点应包括对LTE假设下获得的现有结果的进一步验证。
- 鞘层电压和电流路径——这一点应包括对考虑电弧附着区域的 GMAW 过程功率平衡的相应更深入的研究。
- 电弧附着的建立与熔化部分的动力学和表面特性相关——这应包括分析附加热源(如低功率激光辐射)的影响。
- GMAW 电弧中金属蒸气含量的验证——这应包括对金属蒸发和烟雾形成机理的进一步研究。
- 熔池的表面特性和熔体的流动和动力学——这应包括进一步研究凝固过程对熔池的材料转移和电弧影响。
其中一些问题可能需要新的的诊断方法,或者对现有技术(如探针测量)进行大量开发,以扩大其应用范围。
为了更全面地了解不同的GMAW过程,需要对电弧诊断和材料传输的同步应用进行研究。
其他要求和挑战来自于现有诊断对实际焊接条件的有限适用性。
最后,应在以下两个方面开发监控方法:(a)监控缺陷;(b)主动在线控制过程,以提高稳定性和效率。更为细致的内在物理机制研究和更复杂的诊断方法的发展可以用来支持这里。举例来说,金属蒸发和由此产生的辐射与材料传输中的不规则性之间的关系,一旦得到更详细的评估,就可以为提高灵敏度的控制方法提供一个可能的方向。
集合经验模态分解 (Ensemble Empirical Mode Decomposition)
HUANG Y, WANG K, ZHOU Z, et al. Stability evaluation of short-circuiting gas metal arc welding based on ensemble empirical mode decomposition [J]. Measurement Science and Technology, 2017, 28(3): 035006.
https://blog.csdn.net/liu_xiao_cheng/java/article/details/83897034
经验模态分解 (EMD) 是一种新兴的信号分解、滤波、处理和特征提取的方法,但是它存在着两个显著的缺陷,分别是模态混合和端点效应的问题。
经验模态分解的模态混合问题
EMD 分解得到的 IMF 分量往往存在模态混合,造成 IMF 分量不精确。Huang 等认为模式混叠是极值点的选择造成信号的间歇现象。
出现下列情况之一就称为模态混合:
- 在同一个 IMF 分量中,存在尺度分布范围很宽却又各不相同的信号
- 在不同的 IMF 分量中,存在着尺度相近的e信号。
模态混合使得 IMF 分量失去其具有原来单一特征尺度的特征,形成尺度混杂的振荡,因此失去其原有的物理意义。一个模拟信号例子来说明EMD的模态混叠,如图所示,\(x_1(t)\) 是 10 Hz 的正弦波,\(x_2(t)\) 是间歇信号。
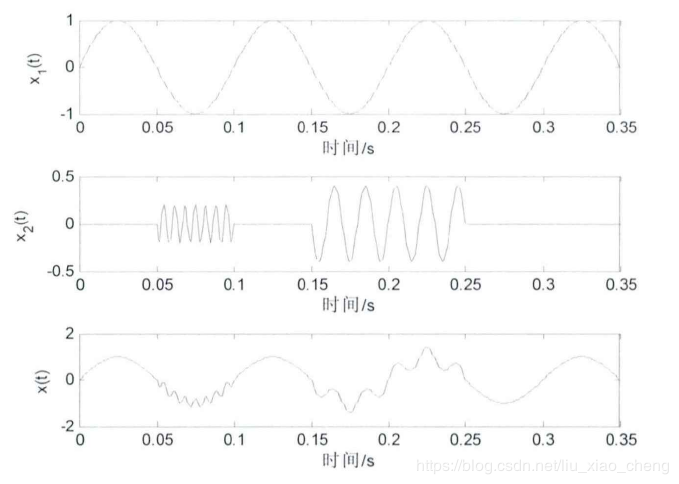
对其进行 EMD 分解得到下图的结果。可以很明显地从图中看出,\(c_1\) 分量中明显存在不同的频率的波形,存在模态混叠现象。
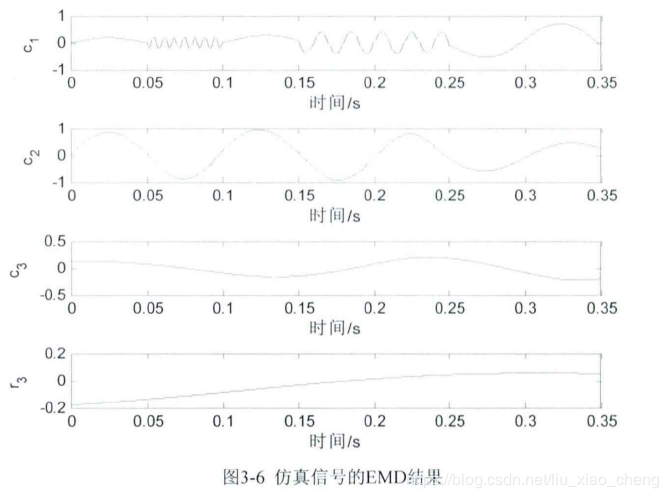
经验模态分解中的端点效应问题
端点效应由两种情形造成的:
- 在三次样条拟合中产生;
- 在Hilbert变换中产生。
端点效应直接影响经验模态分析的效果。端点处理的好,分解的效果就比较好。
集合经验模态分解算法
集合经验模态算法使用均匀分布的高斯白噪声来解决经验模态分解的不足。在经验模态分解过程中,通过多次在信号内引入高斯白噪声,形成一些包含白噪声的内涵模态分量 (IMFs)。对这些 IMF 求取总体的平均值,得到最终的内涵模态分量。而添加的白噪声会在求平均值的过程中被去除掉。
算法实现如下:
假设全局的 EMD 次数为 \(M\),加入的噪声幅值为 \(k\)。
执行第 m 次 EMD 过程:
将幅值为 \(k\) 的白噪声 \(n_m(t)\) 添加入被分析的信号 \(x(t)\) 中: \[ x_m(t)=x(t)+k\cdot n_m(t) \] 其中 \(n_m(t)\) 表示第 \(m\) 次添加的白噪声,\(k\) 是白噪声的幅值,\(x_m(t)\)是第 \(m\) 个原始信号 \(x(t)\) 和白噪声 \(k\cdot n_m(t)\) 的和。
使用 EMD 对添加噪声后的 \(x_m(t)\) 进行分解,得到的 IMF 集合被命名为 \(c_{n,m}(n=1,2,3,\dots,N)\), 即第 \(m\) 次分解的 \(n\) 个 IMFs.
如果 \(m<M\),则使 \(m=m+1\),重复步骤 i 和步骤 ii,直到 \(m=M\)。
最终,\(m\) 次 EMD 的全局平均值 \(y_n\) 可以表示为: \[ y_n=\frac{\sum_{m=1}^Mc_{m,n}}{M}\quad(n=1,2,3,\dots,N\quad m=1,2,3,\dots,M) \] 使用 \(y_n\) 作为最后的分解结果。
如果余项 \(r_n\) 是一个无法再继续进行分解的单调函数,则整个过程的结果为:
\[ x(t)=\sum_{i=1}^ny_i+r_n \]
\(k\) 通常合适的取值范围可以为 0.01--0.5。\(M\) 越大,精度越高,但计算的时间越长。文中的取值为 \(k=0.2,\ M=300\)。
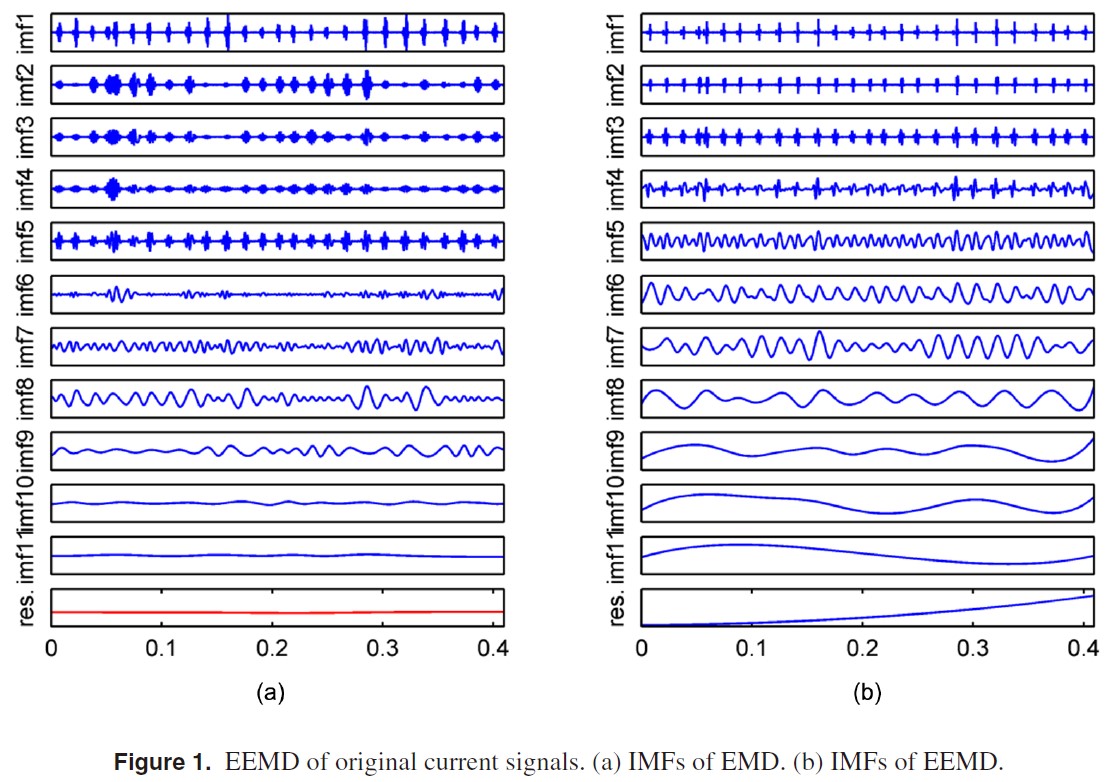
下图展示了 EMD 和 EEMD 对同一原始信号的分解效果比较。显而易见,EEMD 的分解效果更好。