变分模态分解 (VMD)
DRAGOMIRETSKIY K, ZOSSO D. Variational Mode Decomposition [J]. IEEE Trans Signal Process, 2014, 62(3): 531-44.
经验模态分解存在的问题:
高度依赖于极值点查找方法、极值点到载波包络线的插值方法以及施加的停止标准
缺乏数学理论解释,缺少自由度,鲁棒性不足。
变分模态分解(Variational mode decomposition, VMD)是一种针对 EMD 方法的缺陷而进行改进的方法。其主要目标是消除 EMD 方法的端点效应和频率混叠问题。
基本思想和过程
假设目标要将信号 \(f(t)\) 经分解为 \(K\) 个 IMF,其中第 \(k\) 个 IMF 记作 \(u_k (t)\),通过希尔伯特变换可以得到 \(u_k (t)\) 的中心频率 \(\omega_k\)。
则可经过一系列的数学变换得到 VMD 的分析结果。
通过HHT求出原始IMF分量 \(u_k(t)\) 的解析形式: \[ (\delta(t)+\frac{\mathrm{j}}{\mathrm{\pi}t})\ast u_k(t) \]
对上述结果减去中心频率\(\omega_k\),进行标准化: \[ [(\delta(t)+\frac{\mathrm{j}}{\mathrm{\pi}t}\ast u_k(t)]\mathrm{e}^{−\mathrm{j}\omega_kt} \]
对总体的频率带宽进行优化,基于下式:
\[ \min_{\{u_k\},\{\omega_k\}}\left\{∑_k\left\Vert\partial_t\left[(\delta(t)+\frac{\mathrm{j}}{\mathrm{\pi}t}\ast)u_k (t)\right]\mathrm{e}^{−j\omega_kt}\right\Vert_2\right\} \\ s.t. ∑_{k=1}^Ku_k(t)=f(t) \]
经过一定的数学推导,可以得到优化问题的具体迭代过程,如图所示。

VMD的优劣
优势:
分解效果明显优于 EMD 和 EEMD
自适应分解方法,无需选择基波
有完整的数学理论解释
每个子波都处在一个较窄的频带范围之内,子波的物理意义更加明确
允许人为设定分解模式数量 \(K\) 和各模式的中心频率 \(\omega_k\),可通过先验知识提高分解效果
劣势:
需要人为选择分解的模式数 \(K\)
仍然存在边界效应
分析突变型号时效果依然不好
没有余项,不利于分析信号的整体变化趋势
宽带模式分解 (BMD)
PENG Y, LI Z, HE K, et al. Quality monitoring of aluminum alloy DPMIG welding based on broadband mode decomposition and MMC-FCH[J]. Measurement, 2020,158: 107683.
目标:解决信号分解过程中的吉布斯效应等问题,如图所示。
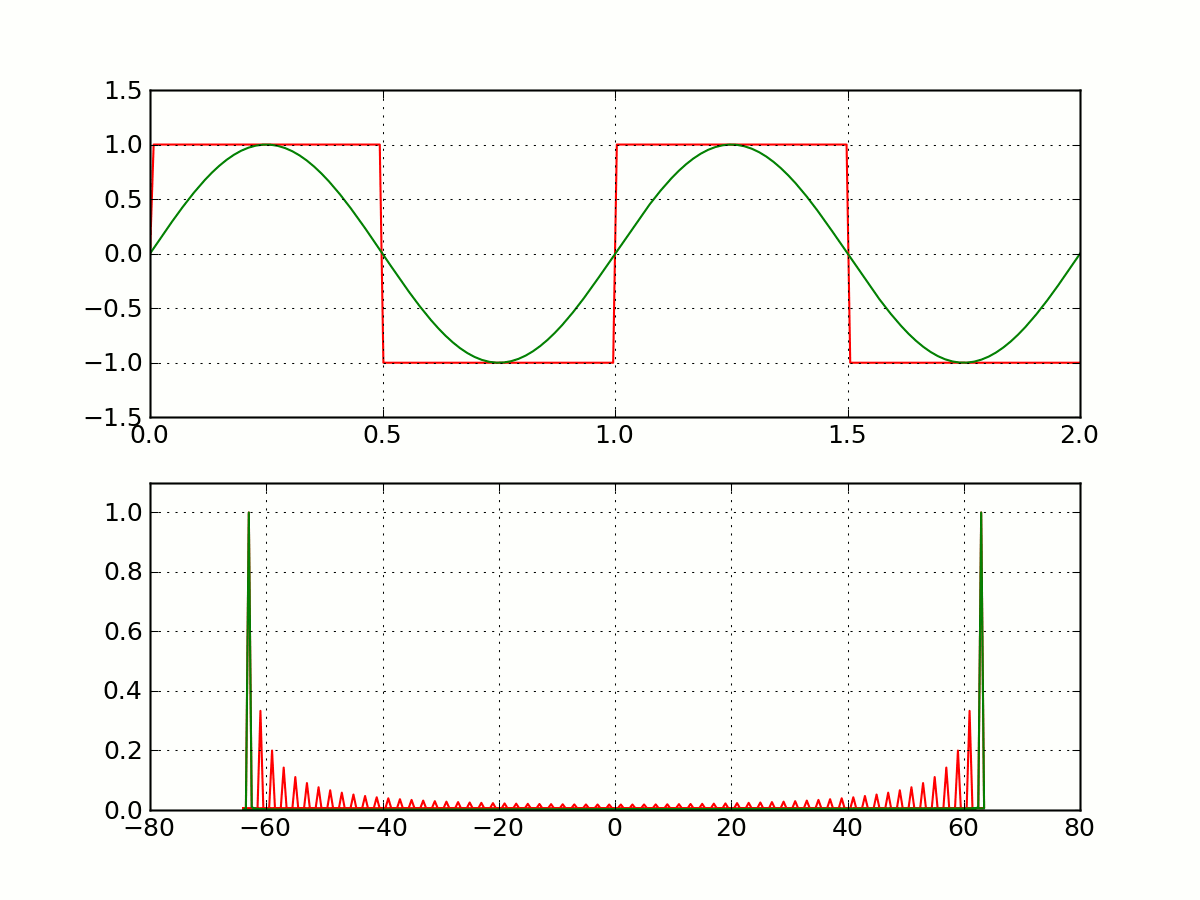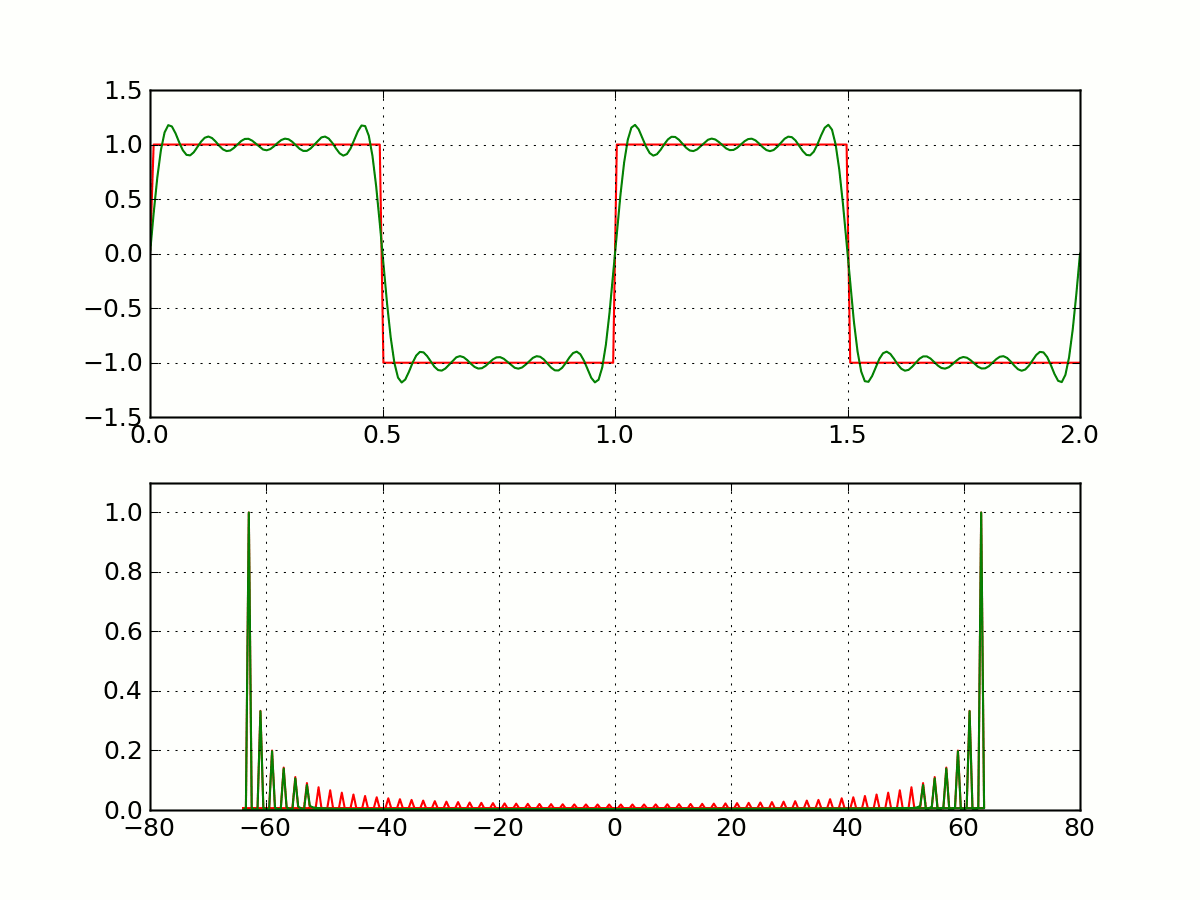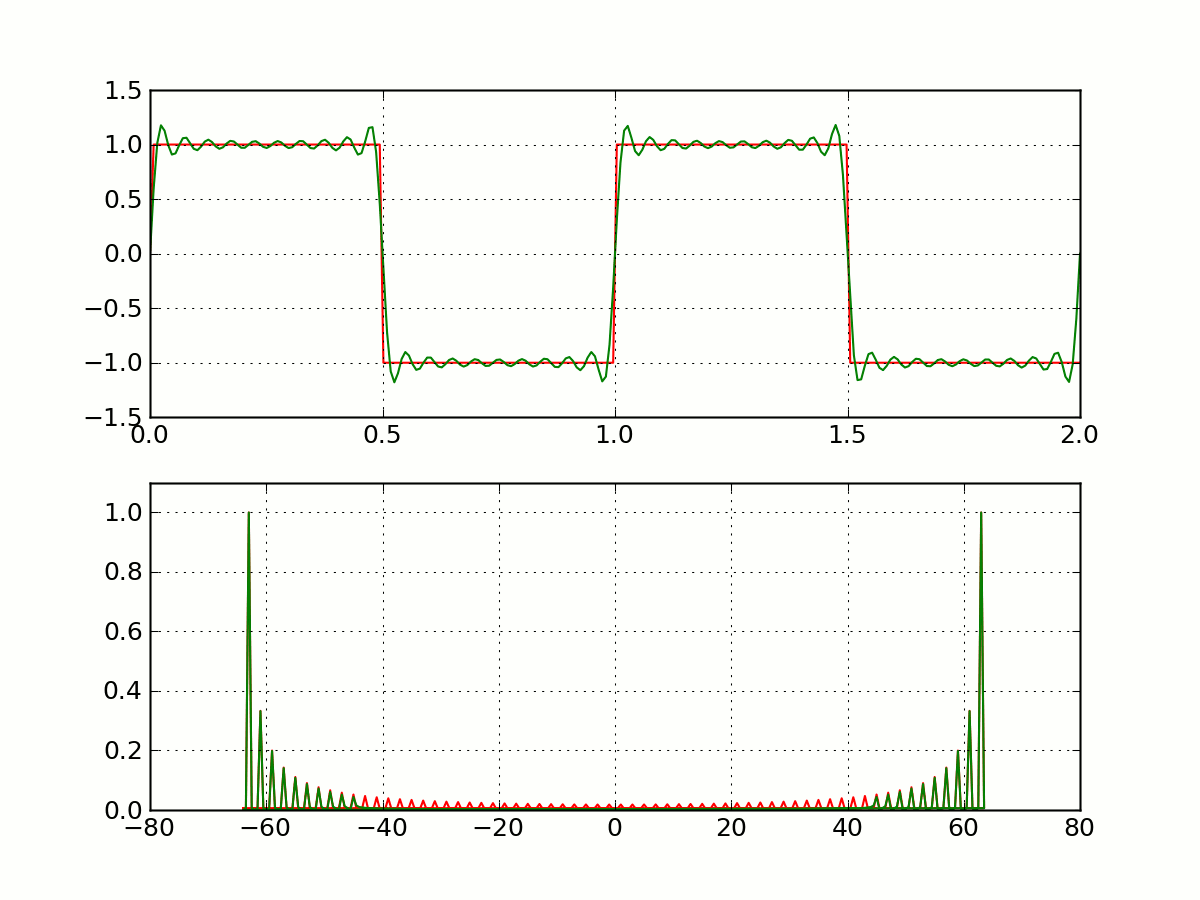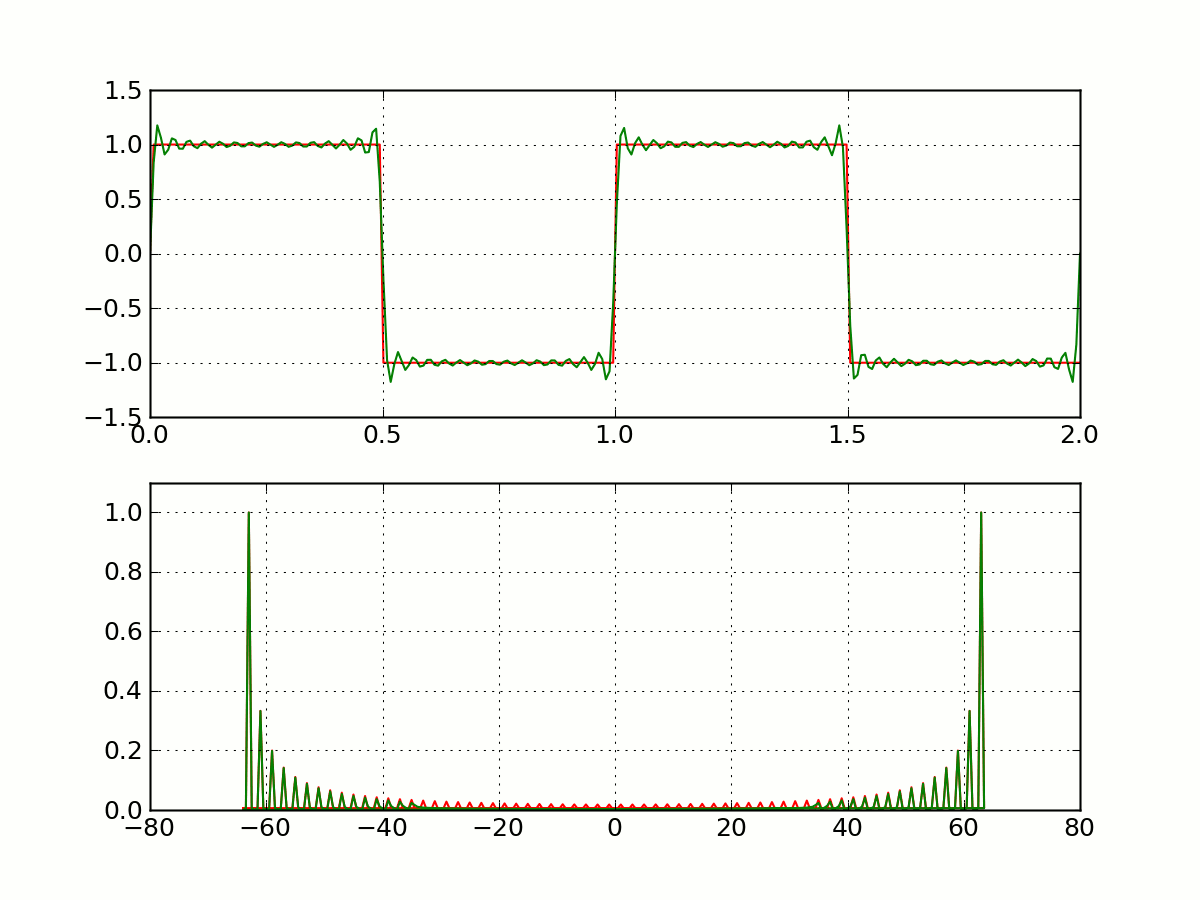
宽带模式分解的基本思路
宽带模式分解 (Broadband Mode Decomposition, BMD)为了将信号中的宽带信号成分和 AM-FM 窄带信号成分从噪声中分解出来,需要建立典型信号字典。
字典包含两个典型宽带信号字典(方波 (square) 和锯齿波 (sawtooth))和一个窄带信号字典:
\[ \begin{aligned} &Dic_1=\left\{A_1\text{square}(\omega_1 t+\theta_1, D_1 )\right\} \\&Dic_2=\left\{A_2\text{sawtooth}(\omega_2 t+\theta_2,D_2 )\right\} \\&Dic_3=\left\{A_3(t)\cos(\omega_3 t+\theta_3 (t))\right\} \end{aligned} \]
其中 \(Dic_3\) 中 \(|A_3 (t)|\ll\omega _3\),\(\theta_3 (t)\) 随时间缓慢变化。 通过在字典中搜索得到分解结果,(优化问题,优化参数为\(A\)、\(\omega\)、\(\theta\))
算法迭代流程
去除直流成分
执行 \(P1\) 优化过程:
优化目标: \[ \begin{aligned} &P1:\min(T_1(A_1,\omega _1,\theta_1,D_1 ),T_2 (A_2,\omega _2,\theta_2,D_2 ),T_3 \left[A_3 (n),\omega _3 (n),\theta_3 (n)\right] ) \\&𝑆.T.\quad x(n)=∑_{i=0}^NIMF_i (n)+rec(n), \quad IMF_i^j\in Dic_j \\&T_j=\left\Vert D^{(2)}\left[IMF_i^j (n)\right]\right\Vert_2^2+𝜆\left\Vert D^{(2)} \left[x(n)−IMF_i^j (n)\right]\right\Vert_2^2 \end{aligned} \]
如图所示
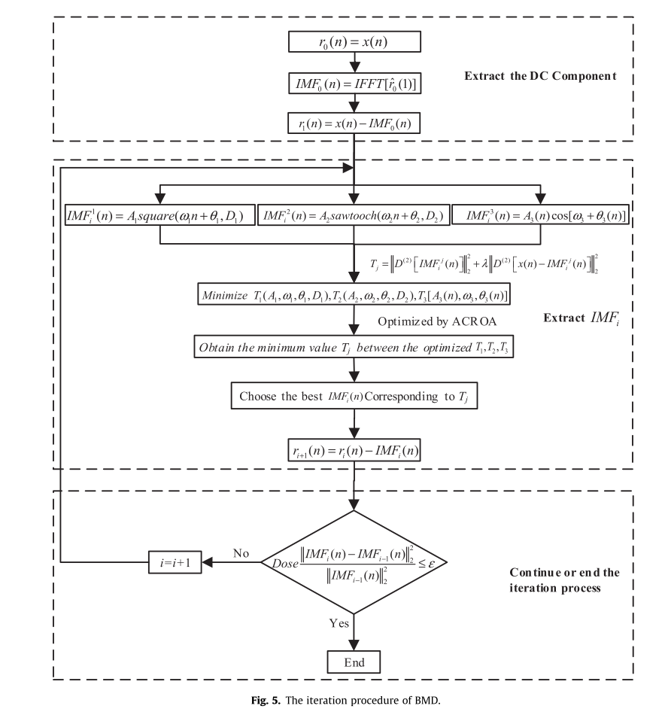
从上述过程可以看到,BMD 方法的主要思路就是在已知信号中含有方波或锯齿波的脉冲成分下,设立对应的字典的分类方法。